Salah satu sifat bilangan real yang penting adalah sifat
Archimides. Penting karena banyak aplikasinya dalam matematika sendiri,
misalnya pada teori ukuran, konstruksi bilangan hyperreal, mencari
supremum atau infimum himpunan diskrit, dan lain-lain. Sifat Archimides
mengatakan demikian,
Untuk setiap terdapat
terdapat 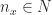 sedemikian sehingga
sedemikian sehingga 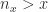 .
.
Menurut saya sifat ini agak aneh meskipun mudah dilihat kebenarannya. Tetapi jika dibalik pun rasanya masuk akal, yaitu untuk setiap bilangan asli terdapat bilangan real yang lebih besar dari bilangan asli tersebut. Cuma pernyataan yang terakhir tidak tahu cara membuktikannya.
Bukti Sifat Archimides:
Andaikan pernyataan di atas salah, artinya terdapat sedemikian sehingga
sedemikian sehingga 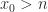 untuk setiap
untuk setiap 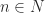 . Ini berarti
. Ini berarti  adalah batas atas himpunan
adalah batas atas himpunan  . Karena
. Karena  terbatas di atas, maka menurut aksioma kelengkapan, himpunan
terbatas di atas, maka menurut aksioma kelengkapan, himpunan  mempunyai supremum. Misal
mempunyai supremum. Misal 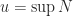 . Jelas bahwa
. Jelas bahwa  , sehingga menurut definisi batas atas suatu himpunan terdapat
, sehingga menurut definisi batas atas suatu himpunan terdapat 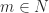 sedemikian sehingga
sedemikian sehingga 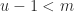 , atau
, atau  . Padahal
. Padahal  . Hal ini kontradiksi dengan fakta bahwa u adalah supremum himpunan
. Hal ini kontradiksi dengan fakta bahwa u adalah supremum himpunan  .
.
Salah satu akibat sifat Archimides adalah
Untuk setiap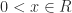 terdapat
terdapat 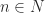 sedemikian sehingga
sedemikian sehingga 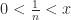 .
.
Sifat di atas dapat dipakai untuk membuktikan bahwa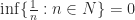 . Caranya begini: Jelas bahwa
. Caranya begini: Jelas bahwa  untuk setiap
untuk setiap 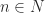 . Ini artinya 0 adalah batas bawah himpunan
. Ini artinya 0 adalah batas bawah himpunan 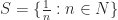 . Dengan demikian, himpunan S dijamin mempunyai infimum. Tidak mungkin
. Dengan demikian, himpunan S dijamin mempunyai infimum. Tidak mungkin  karena 0 adalah batas bawah S. Andaikan
karena 0 adalah batas bawah S. Andaikan 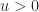 , maka menurut akibat dari sifat Archimides, terdapat
, maka menurut akibat dari sifat Archimides, terdapat 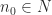 sehingga
sehingga  .
Ini berarti terdapat anggota S yang lebih kecil dari u. Hal ini
bertentangan dengan asumsi u adalah batas bawah (atau infimum) S. Jadi
menurut sifat trikotomi haruslah
.
Ini berarti terdapat anggota S yang lebih kecil dari u. Hal ini
bertentangan dengan asumsi u adalah batas bawah (atau infimum) S. Jadi
menurut sifat trikotomi haruslah  .
.
Untuk setiap
Menurut saya sifat ini agak aneh meskipun mudah dilihat kebenarannya. Tetapi jika dibalik pun rasanya masuk akal, yaitu untuk setiap bilangan asli terdapat bilangan real yang lebih besar dari bilangan asli tersebut. Cuma pernyataan yang terakhir tidak tahu cara membuktikannya.
Bukti Sifat Archimides:
Andaikan pernyataan di atas salah, artinya terdapat
Salah satu akibat sifat Archimides adalah
Untuk setiap
Sifat di atas dapat dipakai untuk membuktikan bahwa

0 komentar:
Posting Komentar